4.2.4 Matriz Inversa

Matriz Inversa.

4.2.3 Propiedades de las operaciones con matrices.

Propiedades de la suma de matrices

 1.  Interna

La suma de dos matrices de orden m x n es otra matriz dimensión m x n.

 2.  Asociativa

A + (B + C) = (A + B) + C

 3.  Elemento neutro

A + 0 = A

Donde O es la matriz nula de la misma dimensión que la matriz A.

 4.  Elemento opuesto

A + (−A) = O

La matriz opuesta es aquella en que todos los elementos están cambiados de signo.

 5.  Conmutativa

A + B = B + A

Propiedades

 1  a · (b · A) = (a · b) · A A  M_mxn , a, b 

 2  a · (A + B) = a · A + a · BA, B  M_mxn , a  

 3  (a + b) · A = a · A + b · A A  M_mxn , a, b  

 4 1 · A = A A  M_mxn

Propiedades del producto de matrices

 1  Asociativa:

A · (B · C) = (A · B) · C

 2  Elemento neutro:

A · I = A

Donde I es la matriz identidad del mismo orden que la matriz A.

 3  Distributiva del producto respecto de la suma:

A · (B + C) = A · B + A · C

 4  No es Conmutativa:

A · B ≠ B · A

Ejemplo

Podemos ver que en este caso, A · B ≠ B · A, de hecho ni si quiera tienen la misma dimensión, pues A · B ∈ M_2x2 y B · A ∈ M_3x3.

4.2.2 Operaciones con matrices.

Suma y diferencia de matrices

Producto por un escalar por una matriz

Producto de matrices

M_{m x n} x M_{n x p} = M _{m x p}

Matriz inversa

A · A^-1  = A^-1 · A = I

(A · B)^-1  = B^-1 · A^-1

(A^-1)^-1  = A

(k · A)^-1  = k^-1 · A^-1

Cálculo de la matriz inversa

4.2.1 Tipos de matrices.

Matriz antisimétrica:

Se trata de una matriz cuadrada que es igual a la opuesta de la traspuesta.

Todos los elementos de la diagonal principal han de ser iguales a cero ya que no existe el , existe el cero. No existe el menos cero ni el más cero. Es un concepto. Existe una pera o no existe una pera. No puede existir la pera.

Conviene leer despacio para no liarnos.

Observa la matriz siguiente:

Se trata de una matriz antisimétrica porque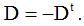  

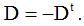
Comprueba y verás que los valores de las filas de la primera coinciden con los opuestos de los valores de las columnas de la segunda.

Ejercicio #5  Si trazamos una línea por la diagonal principal (eje de simetría) y doblásemos por ella el papel ¿coinciden los valores simétricos?
Respuesta: No, coinciden sus valores opuestos.

Matriz escalonada:

Se dice que una matriz es escalonada cuando al principio de una fila hay un cero más que en la fila anterior: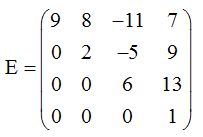

Al principio de la segunda fila hay un cero más que al comienzo de la fila anterior que es la primera.

Al comienzo de la tercera fila hay dos ceros, es decir, uno más que en la fila anterior que es la segunda.

Al comienzo de la cuarta fila hay tres ceros, es decir, uno más que en la fila anterior que es la tercera.

Ejercicio #6   ¿Son escalonadas la matrices A y B:

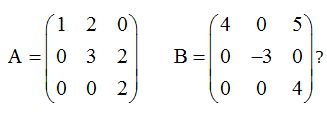
Respuesta: Sí. Los elementos nulos o ceros en nuestro caso, cuentan a partir del comienzo de cada línea.

                     

Ejercicio #7  ¿Es escalonada la matriz:

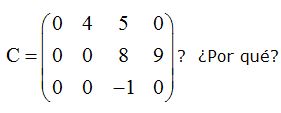
Respuesta: No, porque al comienzo de la tercera fila hay 2 ceros, lo mismo que en la 2ª. Si en la 3ª hubiera tres, entonces sí sería escalonada.

Matriz diagonal:

Es la que todos sus elementos, excepto los que componen su diagonal principal son nulos o ceros: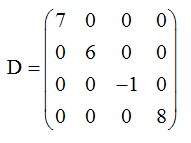

Matriz identidad:

Si todos los elementos son ceros o nulos excepto los que componen su diagonal principal que han de ser iguales a 1: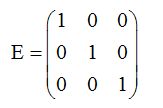

Matriz identidad:

Si todos los elementos son ceros o nulos excepto los que componen su diagonal principal que han de ser iguales a 1: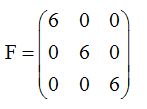

Matriz triangular superior:

Es la que todos los elementos por debajo de la diagonal principal son nulos: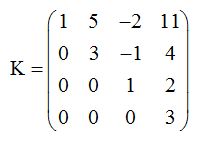

Matriz triangular inferior:

Es la que todos los elementos por encima de la diagonal principal son nulos: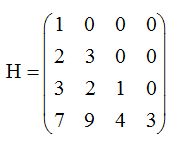

Existen otros tipos de matrices que proceden como resultado de operaciones entre ellas

4.2 Álgebra de matrices.

4.1.5.5 Sistema Homogéneos

4.1.5.4 Reducción de Gauss Y Gauss- Jordan

4.1.5.3 Operaciones elementales sobre renglones.

Hay 3 operaciones básicas usadas en los renglones de una matriz cuando está usando la matriz para resolver un sistema de ecuaciones lineales. El objetivo usualmente es conseguir que la parte izquierda de la matriz se parezca a la matriz identidad.

Las tres operaciones son:

• Cambiar renglones
• Multiplicar un renglón por un número
• Sumar renglones

Cambio de renglones

Puede cambiar los renglones de una matriz para obtener una matriz nueva.

En el ejemplo anterior mostrado, movimos el Renglón 1 al Renglón 2, el Renglón 2 al Renglón 3, y el Renglón 3 al Renglón 1. (La razón para hacer esto es conseguir que el 1 esté en la esquina superior izquierda.)

Multiplicar un renglón por un número

Puede multiplicar cualquier renglón por un número. (Esto significa multiplicar cada entrada en el renglón por el mismo número.)

En este ejemplo, hemos multiplicado el Renglón 3 de la matriz por 1/3. (Esto nos arroja el 1 que necesitamos en el Renglón 3, Columna 3.)

Sumar renglones

También puede sumar dos renglones juntos, y reemplazar un renglón con el resultado.

Por ejemplo, en la matriz que resultó del último ejemplo, podemos sumar los renglones 2 y 3 juntos, entrada por entrada:

Luego, reemplazamos el Renglón 2 con el resultado.

Sumando múltiplos de renglones

Dijimos que únicamente hay tres operaciones, y así es. Pero usando la combinación de las dos últimas operaciones, podemos sumar múltiplos enteros de renglones a otros renglones, para hacer que las cosas vayan más rápido.

Retrocediendo un paso, tenemos la matriz:

Ahora en lugar de solo sumar el Renglón 2 + Renglón 3, sume el Renglón 2 + (2 × Renglón 3):

Luego reemplace el Renglón 2 con el resultado.

De esta forma, obtenemos un 0 en el Renglón 2, Columna 3.

Podemos hacer esto nuevamente para tener un 0 en el Renglón 2, Columna 1. Aquí, multiplicamos el Renglón 1 por –2, sumamos al Renglón 2, y reemplazamos el Renglón 2 con el resultado.

Mostraremos unos pocos pasos más, para obtener la matriz identidad 3 × 3 en la izquierda (y así resolver el sistema).

El paso siguientes es sumar el Renglón 2 + (4 × Renglón 3) para tener un 0 en el Renglón 2, Columna 3.

Enseguida, necesitamos un cero en el Renglón 1, Columna 3.

El último paso es solo una aplicación de la segunda operación, multiplicar un renglón por un número.

Ahora tenemos la solución como una ordenada triple (1, 0, –2).

Nota importante: Si las ecuaciones representadas por su matriz original representan líneas idénticas o paralelas, no podrá obtener una matriz identidad usando estas operaciones de
 renglones. En este caso, la solución o no existe o hay infinitamente muchas soluciones al sistema.